
根据Clark(1957)的“配第-克拉克定理”,当一个产业从资本密集型转变为技术密集型产业,产业增长从中低技术层次转变为高技术层次时,就实现了所谓的产业转型升级。但是近年来的一个典型事实却是,虽然我国制造业结构不断升级,但是工业经济增长的增加值率却不断下降,其原因在于高技术产业增加值率不断下降且低于工业增加值率()。深入到高技术产业内部观察,发现这一现象在IT制造业表现尤为突出(),虽然内资企业进行了大量投入,但在可预期的相当长时期内,整个产业中的技术价值链高地和主要收益部分仍集中于外资企业,内资企业的增长尚没有补偿外资企业增加值的缓慢下降。这意味着外资企业对于整个产业乃至整个制造业的转型升级具有重要影响。我国当前“调结构,稳增长,促改革”的宏观政策环境,以及中美“贸易战”带来的持久性的不可控因素对于一些高技术跨国公司的战略转移起到推波助澜的作用,助推了我国一些制造产业存量FDI的撤离倾向。在整体实力增强的同时,我国制造业不断出现的各类重大创新与技术突破也使得人们对于外资对我国产业转型升级的看法表现出一定的保守态度,外资对制造业的持续发展是否仍然不可或缺,对于产业的转型升级是否有重要影响,实践界与学术界对于这些问题出现了一定的争议。虽然,这一问题可以从国际产业分工、国际价值链等多个理论或者角度予以解读,但在我国当前经济结构转型的关键时期,对于内资企业正在进行的转型升级进程而言,制造业外资在产业层面的撤离会对内资企业发展的稳定性带来多大影响?近年来内资企业高新技术出现井喷现象,是不是意味着内资企业已经可以独立支撑整个产业转型升级进入全球价值链上游?这尤其是我国外资占比较大产业内的内资企业必须警惕,政府在制订产业转型升级政策中必须考虑的重要问题。
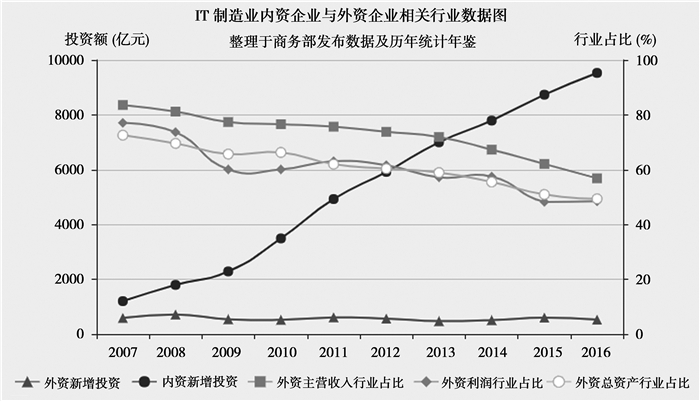
图 1
根据联合国贸发会议的研究,外资撤离通常会影响到1/4到4/5的FDI项目,当撤离发生在不恰当的时机则将会带来不可预料的后果,尤其会增强东道国产业转型的不可控性。但是目前关于撤资影响的相关理论仍不清晰,已有研究主要包括两大方面,一方面是关于外资企业撤离行为的研究,另一方面是关于外资企业撤离对东道国经济影响的研究。
在外资企业撤离行为方面最有影响力的是的撤资条件说。他认为,跨国公司从国外撤资有三个条件:第一,企业不再拥有比其他国家企业更强的竞争优势;第二,企业还拥有竞争性优势,但内部化并不能使企业有利可图;第三,在企业看来,凭借其内部化的竞争性优势在国外进行生产已不再有利可图,即通过出口比对外直接投资更为有利。他将邓宁折衷范式(OLI Paradigm)中的三个对外直接投资前提逆转过来,并且认为,和投资不同,从国外撤资只要具备上述条件中的一个就够了。当外资内化或者本地化带来的优势受到阻碍,无障碍退出就成了撤资最理想的选择。其它研究则可从宏观、产业和企业微观三个层面对企业撤离行为进行梳理。宏观层面研究主要是将东道国经济状态作为企业退出重要变量进行研究。认为企业的撤离行为与经济周期有关,呈反向关联,经济萧条时撤离倾向增加,经济扩张撤离倾向减弱。除经济周期之外,发现外资企业对于市场发展形势的预期也是影响其撤离倾向的重要因素,东道国的经济发展现状在影响市场经营状况的同时,也时刻影响着外资企业对市场发展变化的预期,当其预计未来市场形势恶化,撤离的可能性就会急剧升高。在产业层面的撤离行为研究一般基于产业发展的不同阶段。在产业发展的上升阶段,企业撤离风险较小,的研究证明了这一负相关关系。而在产业发展进入稳定期之后,将产业内企业的进入与退出影响总结为竞争效应和乘数效应,对这两种效应的存在进行了深入研究,并提供了证据。的研究发现,产业的有效规模特征也与企业撤离行为有关,有效规模越大,则撤离的可能性也越高。而在具体企业层面,一般生产率与企业撤离倾向负相关,虽然规模与生产率并不存在明确的正向关系,但、等的研究表明,规模效应显然在声誉、外部资本和生产要素等方面赋予了企业更多优势。的研究还关注了国际贸易与企业撤离倾向的关系,认为出口可以通过调节不同经济周期市场的分配而分散风险,这对于我国外资企业有直接意义,但另一方面也反映了外界波动可对企业造成风险。
在外资企业撤离对东道国经济影响方面,有相当部分的研究聚焦于产业发展方面的影响。认为,规模性的外资撤离会对产业内的东道国企业带来重大冲击,继而影响东道国经济增长与产业转型升级进程。基于1996-2011年我国高技术产业13个细分行业的内资企业和外资企业面板数据,实证发现外资企业与我国高技术产业技术进步之间有显著的非线性关系,证明了内资企业对于外资企业的依赖关系。从技术关联度的角度分析认为外资的进入与退出显著促进内资企业演化,在东部地区的技术关联有利于外资进入带来的知识溢出以及退出带来的资源释放,表现为典型的“战略耦合”。在探究外资对地方企业出口效应的研究中发现,外资注入程度对于提升本地企业的出口份额有明确影响,这一影响与外资流入程度、外资来源的差异以及内资企业类型有不同性质的关系。而随着外资流入程度的降低是否也存在着内资企业绩效降低的问题,这一研究并没有得出相应结论。对于制造业内资企业对FDI的依赖性进行了验证,结果表明2001——2012年间我国绝大多数工业对FDI的市场依赖指数呈现“倒U型”的演化趋势,FDI对东道国市场的依赖指数年均下降0.0048%,行业内资企业规模越大指数下降越快。而的研究则发现,我国外资企业由于学习效应产生的所有权溢价,使得其无条件和条件退出风险均低于内资企业,反映了内资企业对于外资企业的相对弱势。
从理论方面,的产业结构变化理论和的投资发展阶段论可以形成一定的推理逻辑,但是认为,由于东道国内、外资企业间多重因素影响下的复杂关系,外资规模性撤离的后果无论是从资本存量、生产率还是就业角度,对于外资与本土企业的影响机制仍然不是非常清晰。而外国直接投资除了是东道国重要资金来源之外,实际上还与技术进步、人力资源、知识资本等方面有着千丝万缕的复杂联系,影响着投入与产出市场,在要素分配、价格机制、供需机制、生产机制等方面对经济运行产生冲击。相对于计量经济模型,CGE模型有着可靠的经济理论基础,与之匹配的社会核算矩阵(Social Accounting Matrix, SAM)可以将经济体中各个部门纳入统一的框架中,更为全面合理地反映了生产、收入的一、二次分配,以及部门之间的相互联系。尤其是SAM中对部门划分的极大灵活性使我们能够根据研究对象的不同而对部门进行细分,进而分析某一外生冲击对经济体在各个方面的具体影响。
IT制造业是实现我国制造业转型升级的基础推动力之一,对于我国技术进步、经济结构转型、就业岗位容纳等有重要影响,对其内资企业在外资撤离的背景下的表现和转型升级中面临的情形进行深入研究,对于整个制造业具有典型意义。本文基于一般均衡理论,以IT制造业为典型研究对象,将内资企业和外资企业的需求和生产特征进行区分,从资本存量、产出和就业三个方面对IT制造业外资在不同撤离速度情景下对内资企业产生的影响和冲击进行数值模拟,然后将内资企业的劳动生产率进一步分解为技术进步率、技术效率和资本深化深入分析,以探讨和发现外资撤离影响内资企业发展的主要因素和深层原因,进而评估IT制造业内资企业实现和支撑产业转型升级进程的能力,同时为其它类似产业提供借鉴。通过CGE仿真与DEA(Data Envelopment Analysis,数据包络分析)分解方法的结合使用来开展研究是本文与已有研究的主要不同之处之一。
二、CGE模型及数据处理根据一般均衡理论,经济体达到均衡状态依赖于三个条件,即企业利润最大化、居民福利最大化以及市场出清。企业利润最大化和居民福利最大化通常由在一定约束下的最优化问题来表述,而市场出清则表现为每个市场的供求平衡。而我国外资企业与国内企业是具有不同生产特征的生产主体,所以可将其从生产主体中进一步分离;外资企业同样也要在市场上与其它企业进行竞争,比如劳动力和中间品的投入;外资对经济体中不同的产业部门有着不同的影响,也影响着投入与产出市场、消费倾向等。模型构建和设置主要基于以上几个方面的考虑。
(一) 模型构建与设置参考、的基本框架,进一步完善和发展一个开放经济的单国外国投资-CGE模型。外资作为资本要素投入的一部分与国内资本并无本质区分,所以模型按照一般做法仍设计为市场完全竞争、规模报酬不变的四生产部门CGE模型。模型区域由中国和世界其余部分(ROW)组成。在各生产部门中将外资企业作为单独生产主体划分,形成部门内部新的生产主体,包括外国投资变化。模型包括农业、第二产业、第三产业、IT制造业等四个生产部门,一个消费部门、政府部门以及一个代表世界其余部分的ROW部门。根据问题研究需要,模型在已有研究基础上主要做三个方面的工作:(1)除农业外其余三个生产部门分别划分为两部分——内资企业和外资企业;(2)对资本的处理根据特定的要素假设;(3)部门能够对外国投资的流入和流出做出相应反应。模型市场分为商品市场和要素市场两大类,要素市场包括资本要素与劳动要素。国内经济活动参与的主体为居民、国内企业、外资企业与政府,世界其余部分作为一个主体与国内经济主体产生联系。商品市场包括进口、国内企业生产和外资企业进口和生产的各种商品。
在以下CGE核心方程体系描述中,为便于区分,内生变量用大写字母表示,外生变量用大写字母加上横杠来表示,参数用小写字母表示。商品和变量的数量用Q开头,商品价格以P开头,要素价格以W开头;下标c表示商品,i表示经济主体(机构),a表示生产活动,f表示要素,t表示生产主体类型(内资企业、外资企业)。
1. 外资企业生产经济体中各产业部门的国内企业和外资企业使用中间投入、劳动力、资本三类要素生产商品,企业的生产、供给和投入需求通过两层嵌套的生产函数进行描述。在顶层,使用Leontief生产函数将增加值和总中间投入聚合为商品总产出;在第二层包含两个方面, 一是使用Constant Elasticity of Substitution (CES)生产函数将国内企业和外资企业投入的资本与劳动要素复合形成各自增加值并加总,二是总中间投入由国内企业和外资企业的中间投入通过CES函数进行合成;两类企业的中间投入商品通过各自的投入产出固定系数组成,其中中间投入分为国内品和进口品。企业使用规模报酬不变的技术进行生产以及固定定价机制,可以自由进出市场。企业根据其技术和成本约束进行最大化生产,同时其单位成本函数满足零利润条件。从而,可以从成本函数的谢泼德引理中得到中间投入、资本和劳动的需求,并用于市场出清条件中。
关于两类企业的技术差异,认为外资企业的进入能够增加消费者福利,并提升企业生产力,于是在模型中引入了Dixit-Stiglitz-Ethier公式,但是从其模型来看,除却中间产品使用之外,同产业部门内的两类企业技术相同。而等对于两类企业技术差异的考虑则主要基于销售份额和表示资本劳动比率差异的代理变量,同时还假定两类企业的增加值与销售份额比例相同。本文使用企业增加值和产出数据来区分两类企业的技术差异,同时包括各自生产要素投入的替代弹性值或者固定比例系数①。
① 历年《中国统计年鉴》工业部分中可以直接或者计算获得。
方程(1)表示了部门拆分后内资与外资企业生产活动的收入和成本,企业生产的税后收入全部用于支付增加值与中间投入。
$ PA_{a}(1-ta_{a, t})QA_{a, t}=PVA_{a, t}QVA_{a, t}+PINTA_{a}QINTA_{a, t}~~a∈A~~~t∈TD $ (1)方程(2)描述了最大收益条件下内、外资生产部门所必须遵循的CES生产约束,方程(3)则是各部门在此约束下最优生产行为:
$ Q{A_{a, t}} = \alpha _{a, t}^a{\left({\delta _{a, t}^a, QVA_{a, t}^{ - \rho _{a, t}^a} + \left({1 - \delta _{a, t}^a} \right)QINTA_{a, t}^{ - \rho _{a, t}^a}} \right)^{\frac{{ - 1}}{{\rho _{a, t}^a}}}}a \in ACES\quad t \in TD $ (2)在增加值部分的经济活动通过方程(4)进行描述,生产要素投入为资本与劳动力,相应要素价格用WFf, t表示。
$ QV{A_{a, t}} = \alpha _{a, t}^{va}{\left({\sum\limits_{f \in F} {\delta _{f, a, t}^{va}} QF_{f, a, t}^{ - \rho _{a, t}^{va}}} \right)^{\frac{{ - 1}}{{\rho _{a, t}^{va}}}}}\quad a \in A\quad t \in TD $ (4)内资和外资企业的生产为不完全替代,由阿明顿方程(5)进行聚合。
$ Q{Q_c} = \alpha _c^q{\left({\delta _c^qQM_c^{ - \rho _c^q} + \sum\limits_t {\left({\delta _{c, t}^qQD_{c, t}^{ - \rho _c^q}} \right)} } \right)^{\frac{{ - 1}}{{\rho _c^q}}}} $ (5)各产业部门国内企业和外资企业产出的商品QXc, t分配为国内销售和出口两个部分,分配的替代关系由CET函数描述。这一关系及相应的优化条件由方程(6)、(7)和(8)描述。其中ac, tt、δc, tt、ρc, tt分别为CET函数的转移参数、份额参数和指数:
$ Q{X_{c, t}} = \alpha _{c, t}^{ac}{\left({\sum\limits_{a \in A} {\delta _{ac, t}^{ac}} QXAC_{a, c, t}^{ - \rho _{c, t}^{ac}}} \right)^{\frac{{ - 1}}{{\rho _{c, t}^{ac}}}}}c \in CX\quad t \in TD $ (6)模型使用小型开放经济假设,即经济体出口供应函数完全弹性,同时国内、国外的销售使用CET函数表达。对于进口,假设产品根据其来源区分为国内和国外,遵从阿明顿假设,在国际价格外生的条件下允许产业内贸易。外资企业部门的闭合基于以下假设:将ROW收入和支出区别为外生。这一约束会防止出现类似出口持续增长而进口不变的情形,或者是无限制的资本外流。
模型包括两类生产要素:资本和劳动力。其中,资本来源于家庭和公共部门的禀赋,利率在资本不能在国际间和产业间流动的前提下满足国内市场出清,资本外流为外生驱动。同时,资本在两个层面上区分:产业部门和资本来源(公共部门、国内私有和外资)。劳动力要素需求满足家庭部门最优化条件,国际间不可流动,国内部门间可自由流动。
4. 动态模块与宏观闭合模型动态化重在反映出在外资企业参与后,经济体在内部动力(譬如储蓄-投资转换、劳动力增加、技术进步等)推动下经济动态变化的过程。所以,资本要素供应与劳动力供应迭代关联是实现模型动态机制的主要途径,设折旧率和劳动力增长率分别为r和δ,从而得到资本和劳动力的动态递归方程。这一部分的实现主要参考James 的研究。
模型的宏观闭合选择的主要依据是的研究结论:劳动力和资本要素允许失业和自由流动,且投资驱动储蓄。这一具有典型凯恩斯特征的闭合设置能够恰当地反映出在当前的宏观经济条件下,外国投资对于产业部门的要素分配产生影响,从而可以反映其对国内企业的投资效应,以及对资本和劳动力要素在产业部门间,以及在国内企业和外资企业间流动的影响,继而进一步反映出其对内资企业产出和工资水平的变动情况。
(二) 数据基础与相关参数处理 1. 社会核算矩阵结构设计及其数据来源社会核算矩阵(SAM)以2015年中国投入产出表为基础划分部门,将47个生产部门拆分合并为包含农业、第二产业、第三产业、IT制造业(由第二产业中拆分)等4个部门,然后各产业部门拆分为国内企业、外资企业两个生产主体(农业部门缺乏外资相关数据,这里未做划分处理)。国内企业和外资企业进口分为普通消费与中间投入或者投资性进口;中间投入部分,外资企业与国内企业技术差异通过希克斯中性的技术进步体现。
SAM数据处理工作着重于外资企业数据的更新、补全和拆分。各部门外国投资部分的数据拆分主要依据是各部门的外国投资生产数据和销售数据,分别用于拆分内、外企的投入产出和需求数据。外国直接投资部分的数据或者推算数据(比如外企实际税率等)的来源主要是2007、2010、2012、2015年中国投入产出表以及历年《中国统计年鉴》、《中国人口和就业统计年鉴》、《中国信息产业年鉴》和《海关统计年鉴》中的外资企业数据统计部分、《中国国际投资头寸表》、商务部发布的外国投资及外资企业生产及进出口数据①、2003-2016年《中国外商投资报告》、《2010-2014年电子信息制造业运行情况》、《投资中国系列报告》、2004-2016年《中国外资统计》,以及2004和2008年《中国经济普查年鉴》对外国直接投资企业的相关统计数据。
① 商务部:2011-2016年《中国外资统计》,下载地址:, 下载时间2017年6月30日
2. 弹性参数将生产部门进行内、外资企业划分后,对各部门内资和外资部分的生产函数参数进行估计。模型所使用CES生产函数替代弹性参数的估计需要四组经济数据序列:投入资本(K)、资本报酬率(PK)、从业人员(L)、从业人员报酬率(PL)。投入资本K对应数据为资本存量,这一数据使用的待定系数法求得;资本报酬率PK用资本收益(营业盈余)与投入资本的比值来表示;从业人员报酬率PL用从业人员平均劳动报酬来表示;从业人员使用统计年鉴中就业数据、工资数据估算而来。依据这些数据,采用贝叶斯方法对模型所使用的CES生产函数最优条件整理式的参数进行估算,得到各部门内、外资企业的替代弹性,见。
表 1

表 1 内、外资各产业CES生产函数替代弹性值
部门
第二产业
第三产业
IT制造业
弹性值
内资
1.423
0.990
1.536
外资
1.688
2.998
1.066
依据前文对模型需求结构的描述,居民消费支出分别在内资和外资企业产出复合品之间进行最优选择,同时内资和外资企业生产的产品在国内销售和出口之间进行分配。同时,如前所述,这一部分用CET方程和Armington)方程来描述,相应的阿明顿弹性描述的是国内两类企业生产产品和进口品的替代程度,而CET弹性描述的是国内两类企业产品在内销品和出口品之间的替代程度。这里我们假设两类企业产品在内销和出口之间面临同样的替代程度。本文选取等计算的弹性数值,如。内资企业复合品和外资企业复合品的替代弹性在本文中使用设定的值0.1,他们设定此值时假定这两类复合品为有限替代。
表 2

表 2 所选取的Armington弹性和CET弹性值
部门
Armington弹性
CET弹性
第一产业
2.2
3.6
第二产业
2.8
4.6
第三产业
1.9
2.8
IT制造业
4.1
4.6
资本存量、总产出和就业人数的变化趋势通常可以反映一个产业发展稳定性,本部分模拟围绕这三个指标展开。模拟期迭代到2020年,分两步展开:首先结合近年IT制造业外资流入的情况以2015年为基期进行基期模拟,作为后续模拟结果的对比基础;第二步包括以2015年为期初的三种不同规模撤离情景,分别是:情景一、在各期外国投资流入为0;情景二、在外国投资流入为0的情况下外资资本存量每年流出5%;情景三、外资企业资本存量在期初规模性流出25%。三种情景分别对应着我国可能面临的三种不同的外国投资撤离速度的情形。然后将三种方案的模拟结果与基期结果进行对比,分析评估外国投资撤离对内资企业发展和产业转型升级的影响。
(一) 基期模拟以2015年为基期进行模拟时,以当期实际外国投资流入数据为冲击值,模拟结果如所示。与实际数据相比,两类企业的资本存量、总产出和就业人数的增长率模拟值与实际值较为接近,随着模型不断迭代,内资企业的资本存量增加在模拟期内相较外资企业,其增长水平平均达到18.61%,而外资企业的增量则为5.33%,内资企业在各指标方面均超过外资企业。在之后的模拟期,与我国情况基本一致,模拟结果可用于参考基准进行对比分析。
表 3

表 3 基期模拟下内资与外资企业的增长水平变化情况(单位:百分比)
模拟期
资本存量
总产出
就业人数
内资
外资
内资
外资
内资
外资
2015
21.74
3.25
22.51
-0.07
6.93
-3.66
2016
18.3
5.52
20.82
-0.60
7.30
1.15
2017
17.0
6.00
20.39
2.30
8.08
1.09
2018
16.9
5.22
19.15
3.37
7.82
0.13
2019
16.8
3.91
19.89
4.33
6.39
0.78
2020
17.5
4.57
18.77
3.61
6.75
1.04
平均值
18.61
5.47
20.84
2.94
7.27
-0.45
情景一:
如,与基期模拟结果相比,当各期外国投资流入降为零时,后5期内资企业资本存量仍能够较快增加,平均达到21.53%的增长率,但在后期增长水平趋缓,最低为17.90%;总产出变化情况与资本存量相近,在后期增长率仍达到18.01%,平均21.86%;就业人数增长基本保持在8%以上,增长率在中期达到9.8%后回落到8.75%,总体超过基期值。外资企业方面,除就业人数持续按-2.65%的速度下降之外,资本存量和总产出保持较低速率增长,就业人数各期平均下降2.65%。
表 4

表 4 外国投资流入降为0时内资与外资企业增长水平变化(单位:百分比)
模拟期
资本存量
总产出
就业人数
内资
外资
内资
外资
内资
外资
2015
25.70
2.08
26.17
-1.44
8.10
-2.06
2016
22.63
2.32
23.90
-0.60
8.30
-1.15
2017
23.00
2.28
23.48
0.83
9.08
-2.09
2018
20.01
1.90
20.15
1.47
9.82
-3.53
2019
19.93
1.78
19.47
2.03
8.39
-3.10
2020
17.90
1.70
18.01
1.99
8.75
-4.01
平均值
21.53
2.01
21.86
0.71
8.74
-2.65
模拟结果证实了通常外国投资除了直接促成产业资本存量增加之外,会对内资企业投资产生挤入效应。模拟结果中内资企业资本存量和产出的增长率在各个模拟期都保持了较高的增长水平,但在后期表现出下降的趋势,反映出内资企业持续发展的长期稳定性受到FDI的影响。但结合就业人数增长率仍然保持上升趋势来看,相比早期内资企业面临的资金不足问题而言,在当前资金已经不再是制约内资企业发展的重要问题,外资企业持续的技术溢出相对资金更为重要。与多数已有研究结论一致,外资对于IT制造业内资企业的产业投资效应更多地表现为挤入效应,但当FDI持续流入为0时,这种挤入效应的减弱会逐渐趋于明显,从而降低内资企业长期增长的稳定性,对产业实现转型升级产生不利影响。
情景二:
如,当外资资本存量每年持续性减少5%时,外资企业受资本撤离影响各指标均表现为负增长,虽然外资资本存量在各期均比上一期减少5%,但资本存量和总产出的增长抵消了部分减少,并且这种减少并未表现出持续性,甚至在整个模拟期表现出一定的稳定态势,反映出外资企业在产业中的稳固主导地位,这与外资企业近年来虽然资产占比不断下降但主营收入占比仍然相对稳定的现实情况相一致。同时,内资企业方面,各指标值表明内资企业尤其在初期并未对外资的撤离表现出明显的负面影响,各指标水平高于基期模拟值。这一结果可能表明内资企业在一定程度上可能受益于这一情况,即可能对外资企业的撤离进行了替代,从而在初期表现为稳定甚至上扬态势。内资企业各指标值的高增长水平进一步支持了模拟情景一中的结论。但是,内资企业资本存量和产出在后期仍然表现为下降趋势,与其在情景一中的表现相似,意味着内资企业的持续性发展仍然依赖于外资企业,内资企业想要实现长期的市场替代仍缺乏足够的内部支撑。同时,从要素价格变化的角度,近年来劳动力价格的上升推动了资本-劳动相对价格的变化,对外资撤离起到推动作用,但对内资企业的影响却不如预期,反而表现出相当的稳定性。一方面可能是由于资本对劳动要素替代性升高,另一方面可能是由于内资企业与外资企业的从属关系不断减弱导致。
表 5

表 5 外国投资按年5%持续性撤离时内资与外资企业增长水平变化(单位:百分比)
模拟期
资本存量
总产出
就业人数
内资
外资
内资
外资
内资
外资
2015
22.70
-3.11
17.23
-2.77
10.11
-5.06
2016
21.30
-2.52
17.01
-1.96
10.73
-6.89
2017
20.00
-0.65
17.88
-1.31
11.08
-6.60
2018
20.90
-2.09
18.68
0.91
12.52
-7.13
2019
19.30
-2.66
19.35
-2.38
10.69
-6.57
2020
18.90
-2.57
19.79
-1.92
10.66
-5.44
平均值
20.30
-2.27
18.32
-1.57
10.96
-6.28
情景三:
结果与基期模拟相比,当外国投资存量在期初一次性撤离25%时,在期初外资企业资本存量和总产出快速下降,但在后期表现出较为稳定的回升趋势,同时就业人数却一直下降。这一情况与前两种情景中对外资企业产业的判断是一致的,外资企业虽然经历规模性撤离,但仍对整个产业保持主导性。正是由于外资企业是整个产业的技术溢出来源,所以即便其在面临较大规模的撤离后仍能保持相当的稳定性。而内资企业方面,各项指标值大幅下滑如同直觉判断和预期,但与5%规模持续性撤离时模拟的结果不同的是,其在后期的趋势并没有表现出企稳,而是持续下滑。这表明,在这一模拟情景下,外资短期内的规模性撤离对内资企业的发展产生了较强的持续负面影响,内资企业的可持续性发展受到不可承受的负面影响。外资企业各项指标在模拟后期的稳定回升也继续强化了其对产业的稳定支撑作用。与外国投资小规模持续撤离时内资企业发展所表现出的积极性相比,当外国投资短期大规模撤离时,内资企业缺乏长期填补外国投资撤离留出的市场空缺、就业岗位等的能力。虽然内资企业资本各指标增速仍然较快,但与基期值相比,其发展的可持续性和实现转型升级的可能性受到较大影响。
表 6

表 6 外国投资撤离25%时内资与外资企业增长水平变化(单位:百分比)
模拟期
资本存量
总产出
就业人数
内资*
外资*
内资*
外资*
内资*
外资*
2015
15.70
-22.01
17.23
-20.51
6.72
-14.70
2016
14.30
-21.55
17.01
-18.54
6.11
-15.40
2017
13.43
-18.65
17.88
-17.64
6.37
-16.10
2018
11.90
-15.09
18.68
-15.77
5.92
-16.13
2019
11.27
-14.96
19.35
-13.31
5.09
-17.57
2020
10.76
-13.27
19.00
-10.56
4.56
-18.44
平均值
12.89
-16.70
18.19
-16.06
5.80
-16.39
*注:与期初相比。
上述不同情景模拟的结果反映了外资撤离对内资企业从资本存量、总产出和就业人数三个方面的发展趋势和情况,但是对于外资撤离影响内资企业发展转型升级的深层原因和影响机制仍不能给予解释。从当前研究文献看,技术进步、技术效率、资本深化是制造业劳动生产率变化的源泉和动力(; ; ),本文尝试继续从这三个方面对内资企业在模拟期不同外资撤离速度情景下的影响情况进行分析和讨论。在前述模拟结果的基础上,使用非参数DEA方法将各模拟期的劳动生产率分解为技术进步率、技术效率和资本深化率,进而深入观察和分析内资企业在不同外资撤离速度情景下生产效率的演化,进而探讨和衡量其转型升级进程的可持续性问题。DEA方法由A.创建,结合了数学、经济学和管理科学等多个学科,主要利用数学规划模型来对多输入多输出问题中决策单元间的相对有效性进行评价。使用DEA方法和模型可以确定生产前沿面的结构、特征和构造方法,是一种非参数统计估计方法。
(一) 生产技术与生产前沿面 1. 各期生产技术的确定对于各期生产技术可能性的确定主要是对各个生产单元技术过程的描述。假设有S个生产单元,T个生产活动期、N种要素以及M种产出。设投入为X∈R+n,产出为Y∈R+m,则有第s个生产单元在第t期可能的生产技术为:
$ \begin{array}{l} {S^t} = \{ \left({{X^t}, {Y^t}} \right) \in R_ + ^2:x_n^t \ge \sum {{\lambda ^{s.\;t}}} x_n^{s.\;t}, n = 1, 2, \cdots, \\ N;y_m^t \le \sum {{\lambda ^{s.\;t}}} {y^{s.\;t}}, m = 1, 2, \cdots, M, {\lambda ^{s.\;t}} \ge 0, \forall s\} \end{array} $ (9)其中变量λs.t为技术效率权重变量。上式包含了t期所有可能的投入产出组合,在具体计算跨期生产力涉及到的四个产出距离函数时,为了避免出现难以解释的技术退步结果,会将上一期生产前沿面中的点也包括进来。这一做法的主要原因在于,在时间维度上通常在前期能实现的生产技术在后期也能够实现,从而保证所有可能的生产技术在整个分析期内保持一致性,即通过包络分析将上期实际投入和产出数据在前沿面上投影点与当期实际数据一起形成当期的生产技术可能性集合。
2. 生产前沿面的确定根据前面的定义,第s个生产单元在第t期的时投入产出关系为Yt(Xt)=F(Xt, s, t),函数F满足二阶连续可导、单调递增性、凹凸性和规模报酬不变性。在这一函数关系下生产单元达到最优技术状态时,便是达到最小投入最大产出的帕累托最优,所以生产前沿面即为所有生产技术可能性为约束的线性多目标规划的帕累托面,也是DEA面中的有效部分,则有:
$ \overline{Y^{t}}\left(X^{t}\right)=F\left(X^{t}, \bar{s}, \bar{t}\right) \geqslant Y^{t}\left(X^{t}\right) $ (10)根据的定义,当给定技术特征和要素投入时,生产单元的实际产出与最大理想产出之间的比值为技术效率,则其定义为:$ e=Y^{t}\left(X^{t}\right) / \overline{Y^{t}}\left(X^{t}\right)$。则企业在第t期时的实际投入产出与技术可能集St间的谢泼德距离函数可定义为:
$ \mathrm{D}_{0}^{t}\left(X^{t}, Y^{t}\right)=\inf \left\{\theta:\left(X^{t}, Y^{t} / \theta\right) \in S^{t}\right\}=\left(\sup \left\{k:\left(X^{t}, Y^{t} k\right) \in S^{t}\right\}\right)^{-1} $ (11)由于各期投入产出组合(Xt, Yt)∈St,则有D0t(Xt, Yt)≤1。(Xt, Yt)落在St生产前沿面上的投影为(Xt, Yt/D0t(Xt, Yt))。同样,跨期的谢泼德距离函数则可以进一步表示为:
$ D_{0}^{t}\left(X^{t+1}, Y^{t+1}\right)=\inf \left\{\theta:\left(X^{t+1}, Y^{t+1} / \theta\right) \in S^{t}\right\}=\left(\sup \left\{k:\left(X^{t+1}, Y^{t+1} k\right) \in S^{t}\right\}\right)^{-1} $ (12)把Malmquist指数与DEA方法相结合来对一国的全要素生产率的变化进行测度和分解。进一步依据这一研究思路建立了基于DEA的劳动生产率变化分解框架,构造了世界生产前沿,将各国劳动生产率的增长分解为技术进步、技术效率变化和资本积累三个组成部分,并据此讨论经济增长的收敛性。为了在前述模拟结果的基础上进一步分析不同外资撤离速度情景下IT制造业内资企业劳动生产率增长率不同贡献部分的变动情况,在此DEA分析框架中将CES生产函数投入要素分别为资本K和劳动力L,总产出为Y。则令y=Y/L表示劳动生产率,令x=K/L代表资本深化程度。以资本深化程度xt代表投入,以劳动生产率yt代表产出。根据、等的分解框架,在界定第t期生产技术、生产前沿面以及技术效率和相关约束后,第t期到第t+1期劳动生产率变化速度为:
$ \frac{\mathrm{y}_{t+1}\left(x_{t+1}\right)}{y_{t}\left(x_{t}\right)}=\frac{D_{0}^{t+1}\left(x_{t+1}, y_{t+1}\right)}{D_{0}^{t}\left(x_{t}, y_{t}\right)} \frac{\overline{y_{t+1}}\left(x_{t+1}\right)}{y_{t}\left(x_{t}\right)} $ (13)其中,$\overline{\mathrm{y}_{t+1}}\left(x_{t+1}\right) $和$\overline{\mathrm{y}_{t}}\left(x_{t}\right) $分别表示第t期到第t+1期生产活动中投入要素xt和xt+1在生产前沿面技术前提下的最大可能产出。D0t(xt, yt)表示第t期生产前沿面的技术效率水平,则有$\frac{D_{0}^{t+1}\left(x_{t+1}, y_{t+1}\right)}{D_{0}^{t}\left(x_{t}, y_{t}\right)} $为技术效率比率,其大于或者小于1表示技术进步或者衰退。$ \frac{\mathrm{y}_{t+1}\left(x_{t+1}\right)}{y_{t}\left(x_{t}\right)}$大于或者小于1则表示劳动生产率增长或者下降。对方程(13)分别引进跨期最大可能生产水平$ \overline{\mathrm{y}_{t+1}}\left(x_{t}\right)$和$ \overline{\mathrm{y}_{t}}\left(x_{t+1}\right)$,则有:
$ \frac{{{{\rm{y}}_{t + 1}}\left({{x_{t + 1}}} \right)}}{{{y_t}\left({{x_t}} \right)}} = \frac{{D_0^{t + 1}\left({{x_{t + 1}}, {y_{t + 1}}} \right)}}{{D_0^t\left({{x_t}, {y_t}} \right)}}\frac{{\overline {{y_{t + 1}}} \left({{x_{t + 1}}} \right)}}{{\overline {{{\rm{y}}_{t + 1}}} \left({{x_t}} \right)}}\frac{{\overline {{y_{t + 1}}} \left({{x_t}} \right)}}{{\overline {{{\rm{y}}_t}} \left({{x_t}} \right)}} $ (14)其中,则$ \frac{\overline{y_{t+1}}\left(x_{t+1}\right)}{y_{t}\left(x_{t+1}\right)}$表示了在投入产出(xt+1, yt+1)时t到t+1期前沿技术面的变化,同时也可以反映这一技术面发生变化时劳动生产率的变化情况。当$ \frac{\overline{y_{t+1}}\left(x_{t+1}\right)}{y_{t}\left(x_{t+1}\right)}$大于1,则生产前沿面在技术推动下前移,小于1时后退,分别意味着跨期的技术进步与倒退。在本文中,由于会对多生产单元进行同时评价,相邻时期不同单元的数据会导致不同结果,此处参考Fisher理想指数构造方法用两式的几何平均值来衡量模拟期变化,得出式(16)。
$ \begin{array}{l} \frac{{{{\rm{y}}_{t + 1}}\left({{x_{t + 1}}} \right)}}{{{{\rm{y}}_t}\left({{x_t}} \right)}} = \frac{{D_0^{t + 1}\left({{x_{t + 1}}, {y_{t + 1}}} \right)}}{{D_0^{t + 1}\left({{x_t}, {y_t}} \right)}}{\left[ {\frac{{\overline {{y_{t + 1}}} \left({{x_{t + 1}}} \right)}}{{\overline {{y_{t + 1}}} \left({{x_t}} \right)}}\frac{{\overline {{y_t}} \left({{x_{t + 1}}} \right)}}{{\overline {{y_t}} \left({{x_t}} \right)}}} \right]^{1/2}}\\ {\left[ {\frac{{\overline {{y_{t + 1}}} \left({{x_t}} \right)}}{{\overline {{y_t}} \left({{x_t}} \right)}}\frac{{\overline {{y_{t + 1}}} \left({{x_{t + 1}}} \right)}}{{\overline {{y_t}} \left({{x_{t + 1}}} \right)}}} \right]^{1/2}} \end{array} $ (16)对方程(16)两边取对数,并根据跨期产出距离函数$\overline{\mathrm{y}_{t}}\left(x_{t+1}\right)=\frac{y_{t+1}\left(x_{t+1}\right)}{D_{0}^{t}\left(x_{t+1}, y_{t+1}\right)} $和$\overline{\mathrm{y}_{t+1}}\left(x_{t}\right)= \frac{y_{t}\left(x_{t}\right)}{D_{0}^{t+1}\left(x_{t}, y_{t}\right)}$,将生产率的增长率分解为技术效率、技术进步率和资本深化率之和(分解式省略)。
(三) 因素分解与结果分析然后使用各期模拟的IT制造业增加值、就业人数和资本存量分别对应生产函数中产总产出Y、劳动力投入L和资本K,来求解劳动生产率,再进行分解,分解结果见。
表 7

表 7 2016-2020不同外资撤离情景下内资企业劳动生产率及分解(单位:百分比)
模拟期
基期
FDI流入为零
存量撤离5%
存量撤离25%
BL1
TP1
TA1
KA1
BL2
TP2
TA2
KA2
BL3
TP3
TA3
KA3
BL4
TP4
TA4
KA4
15-16
11.67
2.41
4.05
5.21
9.75
2.37
3.47
3.91
8.95
2.08
2.86
4.01
4.21
0.87
0.59
2.75
16-17
12.01
3.02
3.87
5.11
10.22
2.70
3.13
4.39
9.02
2.43
2.69
3.89
4.03
0.30
0.76
2.97
17-18
11.43
2.29
4.15
4.99
10.79
2.98
3.76
4.05
10.11
2.97
3.29
3.85
3.97
0.22
0.88
2.87
18-19
11.71
2.46
4.09
5.22
11.51
3.37
4.02
4.12
9.93
2.46
3.37
4.10
3.89
0.75
0.85
2.29
19-20
12.08
2.68
4.27
5.13
11.24
3.22
3.95
4.07
9.89
2.47
3.42
4.00
3.93
0.95
0.89
2.09
平均值
11.37
2.34
4.00
5.10
10.44
2.82
3.49
4.12
9.55
2.33
3.21
4.01
4.23
0.58
0.86
3.11
注:BLx、TP、TA、KA分别表示劳动生产率、技术效率、技术进步率和资本深化率。
由中IT制造业内资企业在不同FDI撤离情景下劳动生产率变化的情况,结合之前资本存量、总产出等指标的模拟结果,可以发现与基期结果相比,内资企业劳动生产率对于不同情形和规模FDI撤离的反应均比较敏感。在FDI流入为零和外资存量撤离5%两种情景中,内资企业的生产率均受到显著影响,相对基期表现为不同程度的下降,但在各期保持相对稳定,平均值分别为10.44%和9.55%,与基期平均值相比略低,但动态趋势表现为稳中有升。而在FDI存量撤离25%的情景中,内资企业由于产出和劳动要素投入的剧烈变动,导致劳动生产率与基期相比出现大幅收缩,且在各期表现为下滑趋势,平均仅有4.23%。进一步观察各模拟情景下影响内资企业劳动生产率各分解因素在各期的贡献情况,技术效率、技术进步率和资本深化率在各模拟期均为正值,表明它们都促进了劳动生产率的增长。
1. 资本深化的因素分析自2005年以来,IT制造业内资企业投资一直以超过30%的速度增长,在快速推高其资本存量的同时,也为提高行业整体劳动生产率做出了较大贡献。这一趋势在模拟期也表现出巨大惯性,在外资持续流入为0和撤离5%的模拟情景中,资本深化率对劳动生产率的贡献在各期均在40%左右,延续了基期的基本趋势,但有所下降,这一方面表明内资企业由于技术效率和技术进步的弱化作用而出现资本报酬递减的现象并不严重,内资企业在资本投入方面受外国投资撤离影响较小,这也恰好解释了为什么近年来资本-劳动相对价格的变化对外资撤离起到推动作用,但对内资企业的影响却不如预期;但是另一方面也可能意味着内资企业在技术进步方面仍然不足,内资企业劳动生产率的提高更多地依赖于资本主导的技术引进,而非自我创新。这从中也可以注意到,当外资资本存量以25%的速度快速撤离时,资本深化对整个内资企业劳动生产率的促进作用并不能起到支撑作用。同时由于技术效率贡献率的弱化,造成资本本身的报酬递减,难以支撑产业发展,进而对劳动生产率的促进作用也大大降低。但是从我国IT制造业遇到的国际技术壁垒不断增加的形势而言,通过增加资本投入提升技术能力似乎是一个主要途径。
2. 技术效率的因素分析由于外资企业代表着IT制造业最先进生产技术,所以模拟期前沿面的构造选择外资企业来描绘。根据式(10)和式(11)中的定义,技术效率贡献值为正表示其对生产率的提高有着正向的促进作用,反之则为衰退影响。从模拟数据结果看,内资企业技术效率占比变化体现在横向与纵向两个方面。在横向对比方面,在外资持续流入为0和撤离5%的模拟情景中,整个模拟期技术效率对劳动生产率增长的贡献率由平均2.34%上升为2.82%和2.33%,表现出一定程度增加或者没有变化。总体技术效率仍与生产率相比保持同方向变化,反映其仍保持正向促进作用。在纵向时间维度方面,两种情景下的技术效率的贡献率也呈现改善状态。这意味着,在外资较低速度撤离时,其对行业前沿面推进和生产边界上升的影响并不大,而其产生的市场竞争空间的收缩则给予内资企业更多对新技术学习吸收以及进行“技术追赶”的机会。甚至当外资以25%速度快速撤离时,虽然技术效率贡献率大幅下降,但其变化方向仍与劳动生产率变化方向基本一致。但却技术进步形成“剪刀差”趋势,技术效率对劳动生产率的提高产生衰退作用,表现出IT制造业这一产业进步对于技术进步的依赖性。两个方向的分解结果表明,外资较低速度撤离时内资企业的学习效应在外资企业溢出效应下的影响下仍能保持活跃状态,内资企业的技术效率对于其行业劳动生产率增长具备支撑能力。虽然在外资快速撤离影响下技术效率大幅下降,但其变化方向仍与劳动生产率保持基本一致。
3. 技术进步的影响分析从可以看出,在所有情景中,除外资快速撤离情景模拟后期之外,技术进步率对于劳动生产率变动的贡献值均为正值,且高于技术效率。外资企业多年的技术溢出、新技术扩散以及新设备的投入,使得内资企业确实已经具备一定的技术能力储备,虽然外资撤离产生负面影响,但始终处于技术进步趋势之中,成为行业劳动生产率增长的关键因素之一。结合、和可以看到,当外资以较低速度撤离时,整体的劳动生产率受到一定程度的影响,但模拟期内资企业的技术进步仍保持上升态势,贡献率始终处于30%水平之上。表明此时虽然国外技术人员的引进、外资企业的示范作用以及人员流动的技术扩散作用有所下滑,但撤离的同时也降低了外资企业与内资企业间的竞争程度,内资企业在自身能力积累的基础上尚能够参与推动产业生产前沿面的提升,并得以获得更多机会以填补市场空缺。继续结合数据、和观察可以看到,情景三中外资存量的快速规模性撤离使得劳动生产率出现整体性、大幅度下滑,尤其在模拟后期,技术进步对劳动生产率的贡献率出现低于技术效率的趋势,虽然资本投入贡献率仍然较高,但内资企业已有的技术储备能力即便在大量资本投入下也不足以支撑产业获得高速增长,同时技术效率的贡献也十分有限,表明与外资企业的市场交流是其技术进步的重要来源,IT制造业技术进步才是整个劳动生产率增长的关键因素。不管是以索洛为代表的外生增长理论还是以罗默为代表的内生增长理论,都强调技术进步是经济持续增长的源泉,而对于IT制造业这一外资依赖性较强的产业而言,显然不能预见的外生技术进步与基于“干中学”的技术进步和知识积累同样重要。
图 2

以上对劳动生产率的分解分析进一步验证了前一节对模拟结果的趋势分析,明晰了不同外资撤离速度影响内IT制造业内资企业的基本机制和路径。表明了在可预见时期内外资企业仍是内资企业主要技术进步来源,外资企业与内资企业间仍存在着较强的技术壁垒,内资企业在前沿技术面的匮乏,使得外资撤离主要通过冲击内资企业的技术进步而影响资本深化和技术效率,从而影响内资企业劳动生产率。虽然内资企业通过资本深化有利于其提高发展质量并推动转型升级,但在外资以较高速度撤离时使得内资企业的技术进步受到剧烈抑制而大大约束了资本深化和技术效率的作用。
五、研究结论与启示本文以我国宏观经济运行为背景构建结构化动态CGE模型,以IT制造业这一典型外资高占比产业为研究对象,首先从资本存量、生产率和就业人数三个指标,对IT制造业不同外资撤离速度情景下内资企业发展趋势和产业转型升级可持续性的问题进行了数值模拟,然后使用DEA中的Malmquist指数法对模拟期劳动生产率变化进行分解分析以探索行业内外资撤离影响内资企业的机制和路径。数值模拟的结果表明:①当外资流入为0或者其存量以5%的速度小幅持续撤离时,内资企业受影响较小。较高的资本深化率、技术效率和技术进步使得其能够较快填补市场空白,具备企稳回升的能力。结合近年来我国在IT制造领域不断出现的创新和有国际影响力产品的现象,说明我国IT制造业内资企业在面临外资低速撤离时具备一定的稳定性和产业支撑能力,并且这种能力处于不断加强之中;②但当外资存量以25%的速度撤离时,内资企业由于技术进步率和技术效率的双重下降,将处于不可扭转的持续下滑趋势中,表明内资企业的持续稳定发展无法摆脱外资企业的影响。③继而对劳动生产率的分解分析明晰了外资撤离影响内资企业的机制和路径,证明了外资企业在可见预期内仍然将是内资企业的主要技术进步来源,外资撤离会对内资企业技术进步产生抑制作用,在外资较快速度撤离的情况下,即便内资企业的高资本深化率也不能抵消这一冲击,尤其在后期技术进步对于劳动生产率增长的贡献率与技术效率呈现“剪刀差”,反映出内资技术进步支撑的乏力。这些结论表明我国IT产业近年来出现的大量创新现象对于内资企业发展有积极促进作用,但这些创新尚不能支撑和推动整个产业顺利实现转型升级并继续参与国际竞争。